一、近五年高考集合命题趋势与常考题型分析

集合作为高中数学的基础模块，在高考中常以选择题、填空题形式出现，分值占比约5%-10%。近几年高考命题呈现以下特点：

基础题型稳中有变：集合的基本概念（元素三性、集合关系、运算）仍是核心，但常通过创新设问考查逻辑思维。

含参问题高频出现：结合不等式、方程等，考查分类讨论与临界值分析能力。

实际应用逐步渗透：以生活情境为背景，考查集合语言的实际转化能力。

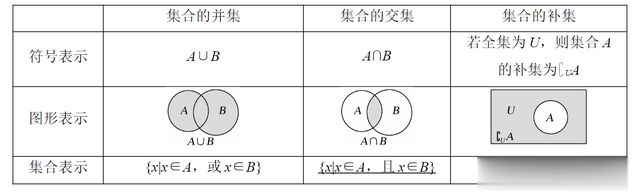
常考题型分类：

题型1：元素特性与集合表示

核心考点：确定性、互异性、无序性

示例（2024全国卷模拟）：若集合{a²,0,-1} = {a,b,0}，则a的值为（ ）

解析：利用互异性排除重复元素，得a²=-1无解或a²=b，结合a≠0，最终解得a=1。

题型2：集合关系与子集问题

核心考点：子集、真子集个数计算，空集的讨论

示例（2024浙江）：已知集合A={x | 1≤x≤3}，B={x | m

解析：需讨论B是否为空集，结合端点值取舍，最终得m

题型3：集合运算与韦恩图应用

核心考点：交集、并集、补集运算，数轴分析法

示例（2023新高考Ⅰ卷）：设全集U=R，A={x | x²≤4}，B={x | x>1}，求。

解析：A=[-2,2]，B=(1,∞)，A∩B=(1,2]，补集为(-∞,1]∪(2,∞)。

题型4：含参集合综合问题

核心考点：参数范围的分类讨论

示例（2024江苏模拟）：集合A={x | x²+ax+b=0}，若A中至多一个元素，求a²-4b≤0的条件。

解析：集合 A是二次方程 x²+ax+b=0的解集。

“至多一个元素”意味着方程的解有两种可能：

无实根（解集为空集，即 A=∅）；

有且仅有一个实根（重根，即 A={}。

根据判别式判断，满足集合 A中至多一个元素的充要条件为：a²-4b≤0.

二、核心知识点深度解析

1. 集合的三要素与表示方法

元素三性：确定性、互异性、无序性。

表示技巧：列举法（适合有限集）、描述法（注意代表元素，如{(x,y)|y=x²}为点集，{y|y=x²}为数集）。

2. 空集的易错点剖析

空集的两重性：① A⊆∅ ⇒ A=∅；② A∪∅=A，A∩∅=∅。

经典错误：忽略方程无解时集合为空的情况，如{x | ax=1}=∅ ⇒ a=0。

3. 集合运算的三大工具

数轴法：适用于不等式集合（如A={x | x>2}，B={x | x

韦恩图：直观展示包含、相交、互斥关系。

德摩根定律：，。

集合的基本运算

三、真题实战与解题策略

案例1：含参集合的交集问题

题目（2024全国卷模拟）：已知集合A={x | x²-3x+2=0}，B={x | x²+ax+b=0}，若A∩B={1}，求a+b的值。

解析：

A={1,2}，由A∩B={1} ⇒ 1∈B且2∉B。

代入1得1+a+b=0；代入2得4+2a+b≠0。

解得a+b=-1，且a≠-3（验证2∉B）。

案例2：实际情境中的集合应用

题目（2025北京模拟）：某班45名学生中，20人参加数学竞赛，15人参加物理竞赛，8人同时参加两项。用集合表示至少参加一项竞赛的学生人数。

解析：

四、备考策略与总结

基础强化：熟记集合的符号语言（如∈, ⊆, ∩, ∪），掌握元素三性的检验方法。

真题精练：重点突破含参问题和端点值取舍，如网页3中“忽略空集导致参数范围错误”的典型例题。

错题归纳：整理易错题型（如混淆点集与数集、漏掉空集），建立错题本。

五、【真题演练】

总结：集合是高考数学的“基石”，其考查方式从单一知识向综合应用过渡。考生需通过真题演练深化逻辑思维，结合题型分类与解析技巧，实现从“知识记忆”到“思维跃迁”的突破。